
Low-magnification views of the night sky can be breathtaking. It’s only with low power that we can fully appreciate the splendor of the Pleiades, the foggy expanse of the Andromeda Galaxy, or the wispy filaments of the Veil Nebula. But if discussions on internet forums are anything to go by, there’s a lot of confusion out there about how magnification, field of view, and exit pupils relate to each other. And without understanding these factors, you might end up shortchanging your telescope’s low-power capabilities.
A low-power eyepiece is likely one of your favorites. Not only is it useful for taking in big targets, it also helps you star-hop from one part of the sky to another as you search for unfamiliar deep-sky objects. But how low can we go? Can we make a 10-inch telescope operate at 10× so that we can harness 78½ square inches of light-gathering power to drink in a huge field of view peppered with faint stars? The answers to these questions lead us to some interesting and underappreciated optical truths.
Less Is More

The singular attraction of low magnification is a wide field of view. The amount of sky you see in the eyepiece is determined by only two things: the diameter of the eyepiece’s field stop and the telescope’s focal length. That’s it. As the photograph at right shows, the field stop is a metal ring normally positioned ahead of the eyepiece’s field lens, though in some complex designs it can be located between lens groups.
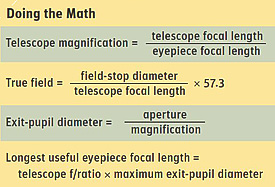
Calculating true field in degrees is simply a matter of dividing the diameter of the eyepiece’s field stop by the telescope’s focal length (both measured in the same units), and multiplying the result by 57.3. For example, an eyepiece with a 27-millimeter field stop used in a telescope with a 500-mm focal length will yield a true field of 3.1° — big enough to take in most of the North America Nebula. As it happens, a 27-mm field stop is about the physical limit for the standard 1¼-inch-diameter eyepiece barrel. So, regardless of its focal length, any eyepiece with a field stop of this size will provide the widest true field possible in the 1¼-inch barrel size.
But what if we want an even wider field? The obvious answer is to go to a 2-inch focuser. This gives us the opportunity to use eyepieces with field stops as big as 46 mm. With our 500-mm-focal-length telescope, we can now get a whopping 5.3° of true field — similar to what binoculars will show.
When it comes to choosing a specific eyepiece, there are additional factors to consider. If, for example, your telescope of choice is a 4-inch (102 mm) f/8 refractor (which has a focal length of 816 mm) equipped with a 2-inch focuser, and you’re looking to buy an eyepiece to give you the widest field possible, you will be shopping for one with a field stop of about 46-mm diameter. Perusing the advertisements in this magazine and on the Web, you find at least two eyepieces that have field stops of that size: a 55-mm Plössl and a 40-mm wide-field design. Since both will yield the same 3¼° true field, which is better? The Plössl will yield 14.8× versus 20.3× for the wide-field ocular. This difference in magnification turns out to be quite important, but to understand how, we need to know the diameter of the resulting exit pupil.
Enter the Exit Pupil
The exit pupil (also known as the Ramsden disk) is simply the image of the telescope’s objective formed by the eyepiece. It is calculated by dividing the telescope’s aperture (in millimeters) by the magnification. In the preceding example, the Plössl produces a 6.9-mm exit pupil (102 / 14.8) and the wide-field eyepiece has a 5.0-mm exit pupil. Since both these values are under the 7-mm limit often cited as the maximum exit pupil usable for the dark-adapted eye, the difference in the view is that the background sky in the 55-mm eyepiece will be as bright as it is with the unaided eye, while it will be slightly darker in the 40-mm ocular. A darker background sky will make many deep-sky objects more visible. So as a general rule, the eyepiece that combines the widest true field with the highest magnification is optimal for low-power viewing.
But what if you have a different telescope, perhaps an instrument with a shorter focal length that is purposely built for wide-field views? Such rich-field telescopes (RFTs) are often f/5 or less. If you had a 6-inch f/4 with a 2-inch focuser, you could get a maximum true field of up to 4⅓° — but there’s a catch. If you used the 55-mm Plössl or 40-mm wide-field ocular to achieve this, you’d end up with either a 13.8-mm or a 10.0-mm exit pupil. If your eye opens up to 7 mm, you will not be taking full advantage of your telescope’s light-gathering capability. Indeed, the 55-mm eyepiece turns your 6-inch into something rather more like a 3-inch scope!
So how do you figure out which eyepiece will combine the lowest power and retain the full light-gathering ability of your scope’s objective? You can calculate the longest-focal-length eyepiece useful for a given scope by multiplying the instrument’s f/ratio by the size of your fully dilated pupil. For the example above of a 6-inch f/4 scope, if you want a 7-mm exit pupil and the maximum true field, you need an eyepiece with a 46-mm field stop and a focal length of 28 mm (4 × 7 mm). Unfortunately, as the graph at right shows, such an eyepiece would have to have an apparent field close to 94°. As far as I know, no one makes such a beast, though Tele Vue’s new 21mm Ethos eyepiece, which features a 100° apparent field, is a good match.
The preceding example leads us to our second general rule: The telescope’s effective aperture sets the upper limit on the maximum true field. In other words, you can’t always get what you want. And that’s too bad. At club meetings and on newsgroups, discussions occasionally crop up in which someone speculates on how great something like the Andromeda Galaxy would look in the famed Palomar 200-inch reflector. In fact, the view would be pretty poor. If the 200-inch were equipped with an eyepiece providing a 7-mm exit pupil, at best you would get a measly 6-arcminute true field — enough to see the galaxy’s core at the seeing-challenged magnification of 762×.
Even using the 21mm Ethos, it simply is not possible to get a true field much greater than about 4½° with a 6-inch aperture, no matter what the f/ratio. And here’s another fact, though less obvious: if your telescope has a 2-inch focuser, it doesn’t need to be faster than f/6 to obtain the widest possible true field for its aperture.
Why is that? Simply because the eyepieces that combine a 46-mm field stop with the shortest focal length are currently models around 42-mm focal length and 70° apparent field. Rearranging the formula for calculating the maximum eyepiece focal length, you can see that with an f/6 scope, you can achieve a 7-mm exit pupil with a 42-mm eyepiece. And as long as that eyepiece has the largest field stop possible, you will achieve the maximum true field possible. However, that is splitting hairs to some degree. You can get a 31-mm-focal-length eyepiece with an 82° apparent field that has a 42-mm field stop: the 31-mm Nagler Type 5. This eyepiece produces a 7-mm exit pupil with an f/4.4 telescope. And with the new 21mm Ethos, you can go as fast as f/3 and still get your 7-mm exit pupil. But the point remains: you don’t need to go faster than f/6 to get the maximum true field with a given aperture — you can still accomplish that goal (and save considerable money) with longer focal-length, less exotic eyepieces.
Getting More with Less

But what if you really want a bigger field of view? As we have already noted, the only way to get more field is to use a smaller aperture. But this might not necessarily mean having two telescopes. Let’s say you do most of your observing with an 8-inch f/4.5 Dobsonian. According to the formula cited earlier, for a 7-mm exit pupil you would use a 32-mm eyepiece (4.5 × 7). If you’re like most people, the only 32-mm 2-inch eyepiece in your equipment box is some kind of Erfle that yields close to a 1° true field. But what if you want to view something really big, like the North America Nebula, which spans more than 3°? Can it be done? Yes — if you have the right eyepiece, say, a 40-mm wide-field type with a 46-mm field stop. You can get 2.9° with your Dob, but such an ocular will yield an exit pupil of nearly 9 mm! This reduces the effective aperture of your telescope to 6¼ inches. Nevertheless, isn’t that better than bringing a 6-inch with you just to have a wider field of view? Certainly a 40-mm eyepiece takes up a lot less room in the car.
So far we have been using a 7-mm exit pupil in our calculations, but this may not be the correct value for you. In fact, most adults’ pupils don’t open that wide — 6 or 5 mm is probably a better figure for most people to use in these calculations. You can measure the size of your fully dilated pupil by holding a ruler next to your dark-adapted eye and taking a picture of your reflection in a mirror. (Your pupil will not contract significantly in the time it takes for the camera’s flash to fire.) Use this result to make your calculations.
Regardless of to how wide your eye’s pupil will dilate, in practice you can use whatever exit pupil your telescope will produce to get as much true field as your telescope is capable of, the principal factor being the size of the eyepiece’s field stop. However, there is another limitation that users of obstructed telescopes need to be aware of. As the size of the telescope’s exit pupil increases beyond that of your eye’s pupil, the area occupied by the scope’s obstruction will increase. You may have noticed this effect in the daytime when your eye’s pupil is quite constricted — the silhouette of the secondary appears as an annoying black spot floating in front of the image. This will happen at night too if the exit pupil is significantly larger than the pupil of your eye.
Going back to our previous example, if our 8-inch f/4.5 has a 30 percent central obstruction (not unreasonable for this kind of instrument), the shadow of the secondary will be 30 percent the diameter of the exit pupil. In other words, fully 2.7 mm of the center of our 40-mm eyepiece’s 9-mm exit pupil would be blocked. But the problem is worse than that. If the pupil of your eye opens to only 5 mm, that 2.7-mm obstruction becomes much more significant and troublesome. Depending on how tolerant you are of this effect and how much you tend to move your eye around while observing, this may or may not be objectionable. However, unlike with refractors and other unobstructed scopes, this is the factor that limits how low you can go if you’re using a fast Newtonian or other obstructed system.
Left unsaid in all this is the importance of optical quality and eyepiece design. While it’s useful to describe theoretical considerations simply in terms of specifications, don’t lose sight of the real world — having the widest true field isn’t the same as having the widest usable true field. If the star images across a significant portion of the field are poor, then what have you gained? There is a reason why eyepieces with wide apparent fields have more elements and cost more than simpler designs with restrictive fields. As always, the best policy is to try before you buy.
Did you find this article interesting or helpful? If so, consider using this link the next time you shop at Amazon.com. Better yet, bookmark it for future use. Thanks to Amazon’s associates program, doing so costs you nothing yet helps keep this site up and running. Thanks!
(This is an updated and expanded version of an article that appeared in the October 2004 issue of Sky&Telescope magazine.)
