
The Newtonian reflector has many strengths, not the least of which is that it consists of just two elements: a precisely shaped paraboloidal primary mirror and a flat diagonal secondary mirror. Yet for all its intrinsic simplicity, confusion abounds when it comes to the optimum size of the diagonal. Many amateurs, and apparently even some telescope manufacturers, seem unsure as to how to choose the correct size for the diagonal. So how big should it be? That depends on several design parameters and some personal preferences.
Making ChoicesSelecting the best size for the secondary mirror of a Newtonian telescope is an exercise in compromise. A diagonal that is too large will block incoming light and exaggerate image-harming diffraction effects, while one that is too small will fail to deliver all the light from the primary mirror to the eyepiece. Certainly, the second of these is the greater evil of the two.
To choose intelligently, you have to first consider what you will be doing with the telescope. Will you be using it for wide-field astrophotography, or exclusively for viewing? Will you be using it to precisely gauge the brightnesses of variable stars, or will this telescope see more duty as a high-resolution lunar and planetary instrument? These questions are important when you are deciding the size of the telescope’s fully illuminated field. To understand what this phrase means and why it is an important consideration, let’s first look at how a reflector telescope works.
In the Newtonian design, all the optical work is done by the primary mirror. It gathers the incoming light and brings it to a sharp focus at the focal plane, where the image is magnified with an eyepiece. The distance from the surface of the primary mirror to the focal plane is the instrument’s focal length. The diagonal mirror simply intercepts the converging cone of light and diverts it out the side of the tube, where the image can be viewed or photographed.
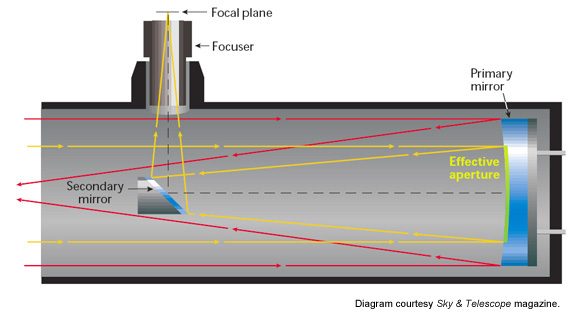
Like a telescope-making Goldilocks, you are looking for a diagonal that is sized “just right” — neither too large nor too small. If it is undersized, some light from the primary mirror will go right past the secondary and out the front of the tube, in effect making the telescope perform as if it had a smaller primary mirror. I’ve tested several commercial Dobsonians that suffered from this malady — one 8-inch scope had a secondary so small that its effective aperture was reduced to 7 inches. On the other hand, a secondary mirror that is too large will also adversely affect the telescope’s performance. Obviously, the larger the secondary mirror, the less starlight will make it to the primary mirror, which is why the secondary is often called the telescope’s central obstruction.However, far more serious than a small loss in image brightness is the resulting reduction in image contrast. A large central obstruction will make it more difficult to see subtle low-contrast detail, such as Jupiter’s wispy equatorial festoons or the delicate surface markings on Mars. The point at which this loss of image contrast becomes noticeable is a matter of considerable debate, but most telescope experts agree that as long as the secondary mirror’s diameter is less than 20 percent that of the primary mirror, its effects should be all but impossible to see.
Finding the Minimum
A good place to start in your quest for the ideal secondary mirror is by figuring the absolute minimum diagonal size that will catch all the converging light rays from the telescope’s primary mirror. To make this simple calculation, you need two numbers: the primary mirror’s focal ratio (f) and the distance from the secondary mirror to the focal plane (L). The focal ratio is simply the telescope’s focal length divided by the diameter of the primary mirror. For example, an 8-inch mirror with a 48-inch focal length would have an f/ratio of 6, or f/6 as it is usually expressed.
To determine L, you need to locate the focal plane. You can find it by removing the eyepiece and projecting an image of the Moon (or a daylight object at infinity) onto a small square of tracing paper taped over the end of the focuser. (A layer of frosted tape will also work for this.) Rack the focuser in and out for best sharpness and measure the distance from the paper to the center of the tube — this is L.

But how do you know that the focal length really is exactly 48 inches? One way to check is to use a clean length of wood or a wooden yardstick, if it is long enough. Slide this down the tube until it just makes contact with the edge of the primary mirror. Next, mark the wood where it crosses the middle of the focuser hole. Measure this distance with a tape measure, and add it to L. This is the telescope’s focal length.To find the minimum secondary size, simply divide L by f. In the case of an 8-inch f/6, L is often about 9 inches. Dividing 9 by 6 gives a minimum secondary size of 1.5 inches. The same telescope with a low-profile focuser rather than the standard tall rack-and-pinion model might have L as little as 6 inches. Such a configuration would allow you to use a diagonal only 1 inch across. In fact, the most effective means of keeping the secondary small is to use a low-profile focuser. For a given telescope, no other design parameter will have as great an influence on secondary size as focuser height.
Bigger May Be Better
While the reasons for keeping the diagonal small are compelling, in practice there are a number of potential drawbacks to going this route. Choosing a secondary that is just big enough means that you are counting on that mirror being perfectly flat right up to the very edge. While such perfect diagonals do exist (most often in the smallest sizes), unless you have some means of verifying the quality of the flat you should not count on it. Second, will the diagonal mirror you purchase really have a clear face of the required size? Diagonals are often listed by the size of the glass substrate, not the effective diameter of the reflective surface. Since the edge of the mirror is beveled to prevent accidental chipping, the actual useful surface might be less than the size given. In addition, how much of the diagonal will the lip of your secondary-mirror holder cover? Taking these factors into account, it is best to purchase a mirror slightly larger than the absolute minimum calculated size.
A minimum-size secondary mirror allows you to take full advantage of your primary mirror’s light-gathering and resolution capabilities — but only at the center of the field of view. Objects toward the edge of the field will receive less than 100 percent illumination and appear slightly fainter. For planetary observing, which is best done with the image of the planet positioned at the center of the field of view, this is usually of little concern, but for more general viewing, fully illuminating a larger portion of the field is usually desirable. For variable-star observing and astrophotography, uniform illumination across a substantial portion of the field is important.
The diameter of the fully illuminated field is usually governed by the size of the secondary mirror. For example, if a ½ -inch fully illuminated field is desired, simply add this amount to the minimum diagonal size to figure out the approximate diameter of the secondary. So, if you have calculated your minimum diagonal size to be 1.5 inches, using a 2 inch secondary will yield a fully illuminated field of ½ inch across.
To determine the approximate size of the fully illuminated field in an existing instrument, simply subtract the minimum diagonal size from that of the actual secondary mirror. A telescope equipped with a 1.83-inch diagonal that requires only a 1.5-inch secondary will have approximately a 0.33-inch-diameter fully illuminated field.
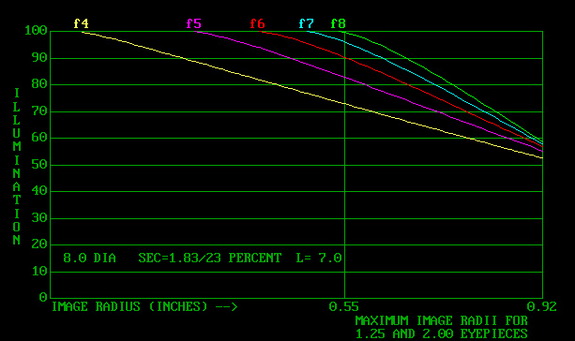
However, choosing a secondary mirror for a given size of fully illuminated field is not the best strategy and can often lead to choices that are not optimal. Instead, I’d encourage you to consider a more “real-world” approach. Namely, for most observers, the size of the fully illuminated field is less important than how much dimming they will see at the edge of the field of view. Generally, the larger the fully illuminated field, the less dimming you will see at the edge of field, but (and this is a big “but”) the illumination drop-off is much more gradual with short-focal-length telescopes than long-focal-length instruments. If your scope is an f/5, you really don’t need to fully illuminate more than the very center of the field —the brightness drop off at the edge will be very difficult to see if you go this route. However, if your have an f/8 scope, you will see more dimming even if you choose to fully illuminate a good portion of the field of view.
Planetary observers tend to be fanatical about keeping the secondary mirror as small as possible and don’t mind if the edge illumination drops to zero. Deep-sky observers, on the other hand, usually prefer wide fields of view with full illumination. For most people, so long as the illumination at the edge of the field doesn’t drop below 50 percent (amounting to roughly ½ magnitude), it will go unnoticed.
A very handy computer program by Alan Adler (called Sec) plots illumination profiles for various combinations and can be downloaded here. This is the best utility I’ve seen of the many out there. I’d avoid using the Dale Keller’s otherwise excellent program Newt for this application since it handles this subject in a confusing manner.
While you should choose carefully after weighing all the various design considerations, don’t lose sleep agonizing over finding the perfect size. For one thing, you might have to settle on a diagonal slightly larger than ideal since these mirrors come only in a limited number of sizes. However, you can rest assured that even if this happens, you are unlikely to be able to see a difference. Of course, if you’re like most telescope makers, seeing the difference is less important than knowing it’s right!
Did you find this article interesting or helpful? If so, consider using this link the next time you shop at Amazon.com. Better yet, bookmark it for future use. Thanks to Amazon’s associates program, doing so costs you nothing yet helps keep this site up and running. Thanks!
Note: This is an updated and expanded version of an article I wrote for the August 2000 issue of Sky & Telescope magazine.
